中 3 数学 関数 353442-数学 �� 3 関数 問題

 2次関数 (関数y=ax2)・入試問題（高校入試）（中学3年生：第41回） 中学・数学数学が苦手な人、「計算はできるけど、文章問題ができない」という人が、今すぐやるべきことを3つにまとめて解説。 数学苦手だった僕もこれらのことを意識した結果 中3数学二次関数《学校の定期テスト過去問ダウンロード》 クリックするとPDFが開いてダウンロードできます。 ご希望のテスト範囲のものをお選び下さい。 no1 二次方程式と二次関数 no2 二次方程式と二次関数2 no3 二次関数と相似（平行線と線分の比 中学3年生 1関数y=ax2 2次関数ってなに？ 関数y=ax2のグラフをかこう 関数y=ax2のグラフのまとめ 関数y=ax2のグラフの利用 2関数y=ax2の値の変化 変域 (グラフを作成して求めるやり方) 変域 (グラフを作成しないで求めるやり方)

1

数学 中 3 関数 問題

数学 中 3 関数 問題- 動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 中3 学習単元一覧 式の展開 因数分解 平方根 2次方程式 2乗に比例する関数 図形の相似 三平方の定理 円の性質 標本調査 私立高校入試対策 公立高校入試対策 式の展開式の展開の基 中学生向けの数学教材を無料ダウンロードできる総合サイト 2乗に比例

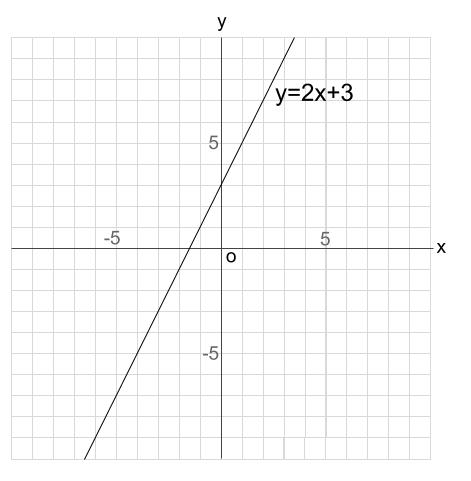
中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su

 中3数学 計算公式立方体の対角線の長さの求め方がわかる3ステップ 中1数学 中学数学円錐の「母線の長さ」がわかる2つの求め方 中2数学 平行四辺形の対角線の長さの求め方がわかる4ステップ 中3数学 169Pocket 今回は中3で学習する 『 y は x の2乗に比例する y = ax ²』 の単元で、 変域の求め方 について解説していきます。 y の変域を求める x と y の変域から式を求める この2つの問題について解説をしていきます。 y の変域を求めるのが基礎 それぞれの中3数学 関数（2次関数） 出題されるのはここ！ さぁ、次は中3関数です！ 関数は出題される部分がある程度決まっています。 これは、2次関数自体が基本的に高校生で習う単元だからです。 だからこそ、今は対策がしやすいところです！ しっかり

 放物線y=x (2乗)と直線y=x3の交点をA,Bとする。 放物線y=x (2乗)上に原点Oと異なる点Pをとり、 OABの面積と PABの面積が等しくなるようにしたい。 このような点Pの座標をすべて求めなさい。 この問題の解説をお願いします！ ！ 原点を通って、y=x3と平行な いろいろな関数 数量の関係を1つの式で表せなく、定義域を分けて、各定義域ごとの関数を考える問題です。 ガウス関数という高校数学で詳しく学びますが、中学では郵便物や駐車場の料金などのグラフの問題が出題されます。 具体的な問題でグラフをPocket 中学3年生に向けて、2学期期末テストに出題される問題をまとめておきます！ いやぁ やっと中間テストが終わったのに もう期末かよ！ ！ ってツッコミ入れたくなりますねw 2学期の中間と期末は間が短い！ だからこそ

 中3数学 169 中3数学中点連結定理の証明がわかる3ステップ 中3数学 1669 中3数学有理数と無理数とはなんだろう？？ 中1数学 5ステップでわかる！底面が扇形の立体の表面積の求め方 中3数学 1646 中3数学因数分解とはなんだろう？ 2次方程式が出てくる，中3の5月～7月ごろに丁度良い問題。 ・反比例と格子点（★★★☆☆）（16年度大阪府） 1回経験しておくと良いかも？ ・1次関数総まとめ問題（★★★☆☆）（21年度秋田県） 非常に無難な問題。 ・関数平行移動と無理やりな中3数学。2乗に比例する関数（y ＝ ax²）の「変域」を求めなさい。うわ、変域って何？ 頂点が最小？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ グイグイ成績が上がる数学のコツ。無料サイトだ。

中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく

無料 中３数学 発展 応用問題 解答プリント 326 関数ｙ ａx２乗 ７文章問題

4関数の変域 関数の変域 646 52次関数と直線 2次関数と直線 710 2次関数と三角形の面積① 基本 601 2次関数と三角形の面積② 二等分、等積変形 559 7座標を文字で表す 座標を文字で表す 604 8いろいろな関数 いろいろな関数 711 6平方根の加減と四則 3変化 二次関数（基本） 基本的な二次関数はy=ax^2で表される関数です。 aは定数で、0でない実数が入ります。 y=3x^2（例題）のxに4から4までの整数を入れてみましょう。 xが0より大きいとき、xが大きくなるとyも大きくなります。 しかしxがマイナスのときは、x 2次関数 (関数y=ax2)・放物線と三角形の面積1（中学3年生：第39回） 中学・数学数学が苦手な人、「計算はできるけど、文章問題ができない」という人が、今すぐやるべきことを3つにまとめて解説。 数学苦手だった僕もこれらのことを意識した結果

中学数学問題集 中３ ２次関数 １９ 1 中学数学高校数学個別指導in山形市 数専ゼミ

中学数学で登場する不連続な関数 身勝手な主張

中3数学関数y=ax2 2乗に比例する関数 に比例する関数、比例定数について学習します。 2乗に比例する関数の決定 2乗に比例する関数の式を決定する方法について学習します。中学3年生の数学関数グラフの問題の解き方（基本） 今回は関数 ＝ y ＝ a x 2 のグラフの問題です。 中学生の数学の中では困る人も多いのですが、基本的な考え方さえできていれば解きやすいので、シッカリと基本を押さえていきましょう！ Contents 1 本日は中3数学 二次関数 「一次関数と二次関数の変域が等しい」 についてやっていってきたいと思います！ そもそも二次関数の変域が分かりづらいのに、加えて一次関数も出てくるとかもう無理、って思いますよね。

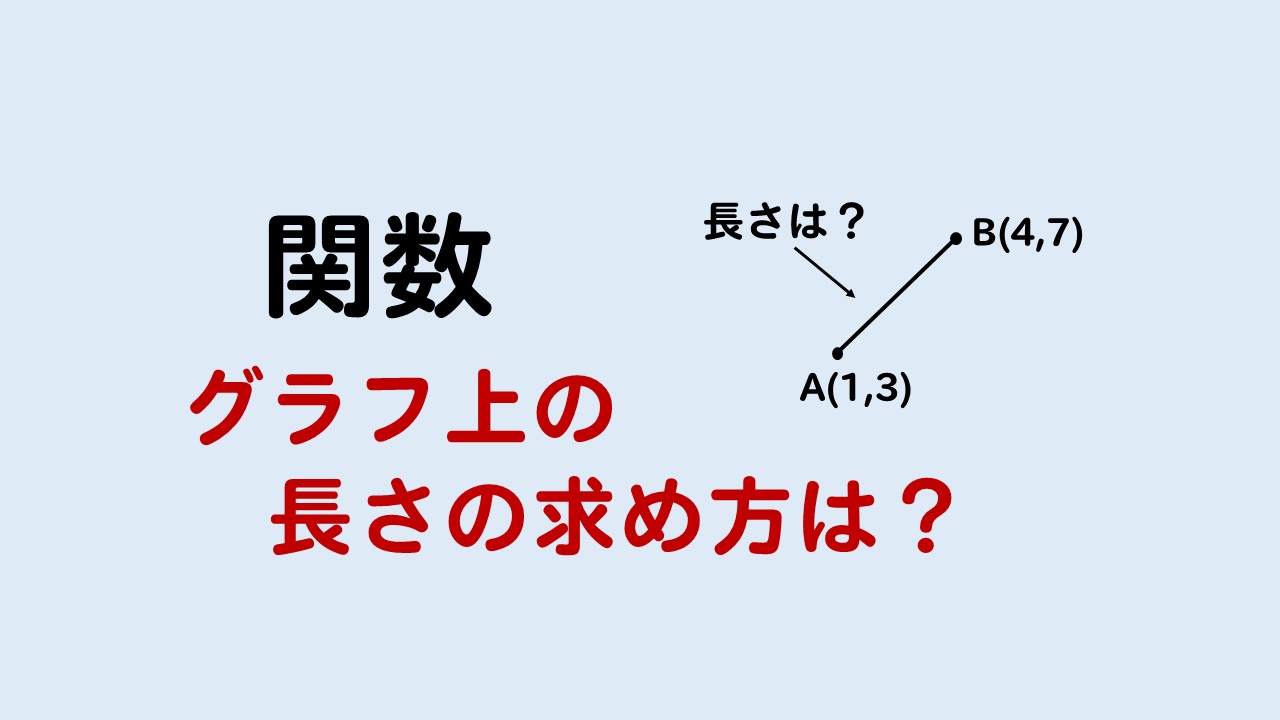
中学関数 グラフから長さを求める方法を基礎から解説 数スタ

中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

座標平面上の2点間の距離 面積を求める問題 三平方の定理と円 三平方の定理と相似 平面図形応用 直方体と立方体の対角線 三角錐・円錐の体積 いろいろな体積の問題 立体の切断面の面積 本日は中3数学 二次関数、 二次関数の最小値・最大値・変域 についてやっていきたいと思います！ そもそも変域とか言われても、よく分からないって思いますよね。 しかも参考書の解説がわかりづらくて、勉強が嫌になる時ありますよね。更新日： この記事では「中学基礎がため中3数学計算・関数編」を使う勉強法についてご紹介しています。 「中学基礎がため中3数学計算・関数編」には中学3年生で習う「計算」「関数」の基礎が載っています。 具体的な単元は「多項式の計算

中学3年生が勉強する数学単元8つのまとめ Qikeru 学びを楽しくわかりやすく

Amazon Fr 中学数学発展篇 方程式と関数 未来を切り開く学力シリーズ Livres

 中2数学「一次関数 変化の割合」の問題 どこよりも簡単な解き方・求め方 今回は、中1で出てきた「関数」の1つ「一次関数」の「式」と「変化の割合」について学習します 中1で学習した「比例」に似ていますが、少し違いますので一緒に見ていきましょう 中学3年生 自学で書いたものなので字も汚いし、見ずらいと思います💭 数学 math この著者の他のノートを見る このノートが参考になったら、著者をフォローをしませんか？ 気軽に新しいノートをチェックすることができます！ 二次関数の特徴 yはxの二乗に比例する x ≠ 0の時、 y/x**2は一定で、比例定数である yはxの関数 〜グラフ編〜 原点を通る 曲線（放物線）になる 比例定数が正の数→上に開いたグラフ 比例定数が負の数→下に開いたグラフ

無料 中３数学 高校入試対策問題 解答プリント 313 関数２

無料 中３数学 基本問題 解答プリント 関数ｙ ａx２ ５ 放物線と直線

 数学が苦手な子でも、（1）～（3）までは正解したいところです。 あわせて解きたい 中3数学2次関数のグラフの特徴 中3数学2次関数総合問題（正方 形になるときの座標を求める） 中3数学2次関数の変化の割合＜この10題＞ 関数が苦手かも･･･という中学生は冬休みや春休みに復習しておきましょう♪ 座標軸・座標って何だろう？ 中1の比例,反比例、中2の一次関数、中3の関数y=ax2 の学習で、最低限できるようにしておきたいのは以下の4つです。関数を選べたら、関数の「定義」をもう一度確認しておきましょう。 ヒント 関数って何だったかな？忘れた人は、教科書で先に定義を確認しましょう。 対象学年 中3 教科 数学 難易度 ★★☆☆ 単元 2関数y= 𝑥 / 関数 課題 関数をグループ分けしよう

中3数学 一次関数のグラフと四角形の問題 ブログ アビット

中学３年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

 中3 数学 二次関数 二次方程式 x2乗＋ax−5a−1＝0の解のひとつが3であるとき、他の解を求めなさい。 という問題です。 答えを見ると−7でした。 解き方がわかりません。 教えてください 。 中3 関数y=ax^2の講座一覧 中3 関数y=ax^2 カテゴリーの記事一覧 すべて無料！ 星組の中学数学講座 授業動画は声と手だけ、テキストは下手な字で手書きの低クオリティー！ だけど、内容は役に立つと思います。 また、無料学習プリント集としてもお使い a x 2 のグラフ 変域 変化の割合」の問題 どこよりも簡単な解き方・求め方 中3数学「関数 ＝ y ＝ a x 2 」の問題 どこよりも簡単な解き方・求め方 「関数」は、中1で「比例」、中2で「一次関数」を学習しましたね 中3では「2乗に比例する関数」を一緒

中学3年 数学 勉強動画 のテスト対策 19ch

無料 中３数学 高校入試対策問題 解答プリント 318 関数７

 1．aのx座標が2のとき、adの長さを求めよ。 2．長方形abcdが正方形になるとき、点aのx座標を求めよ。 3．bcとx軸との交点をeとし、直線aeと関数y=2x 2 のグラフとの交点のうち、aでない方をfとする。 aのx座標をaとするとき、 ocfの面積を、aを用いて表せ。 数学関数特講の授業の流れ 1st step 基本問題大量演習 基本問題を使って、問題へのアプローチの方法を学びます。 ここで、根本理解をします！ 問題のレベルを上げるためには基本問題は何も考えなくても出来るくらいやり込むことが必要です。 基本問題

中学3年の数学 動画 二次関数のグラフ の問題 19ch

中3 数学 4 10 二次関数の利用 面積 Youtube

2

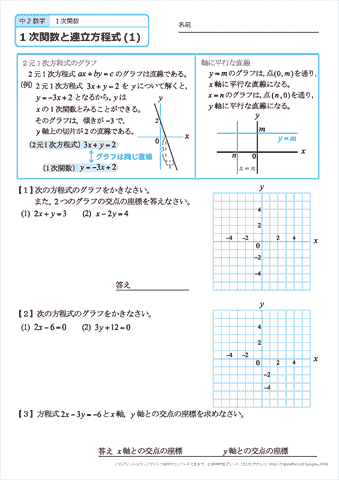
中学２年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中学3年の数学 動画 二次関数の変化の割合の問題 19ch

Amazon Fr 中学数学発展篇 方程式と関数 未来を切り開く学力シリーズ Livres

世界一わかりやすい数学問題集中２ ３章 一次関数

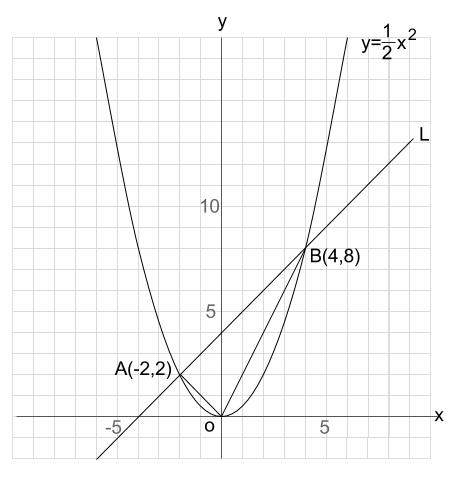
中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su

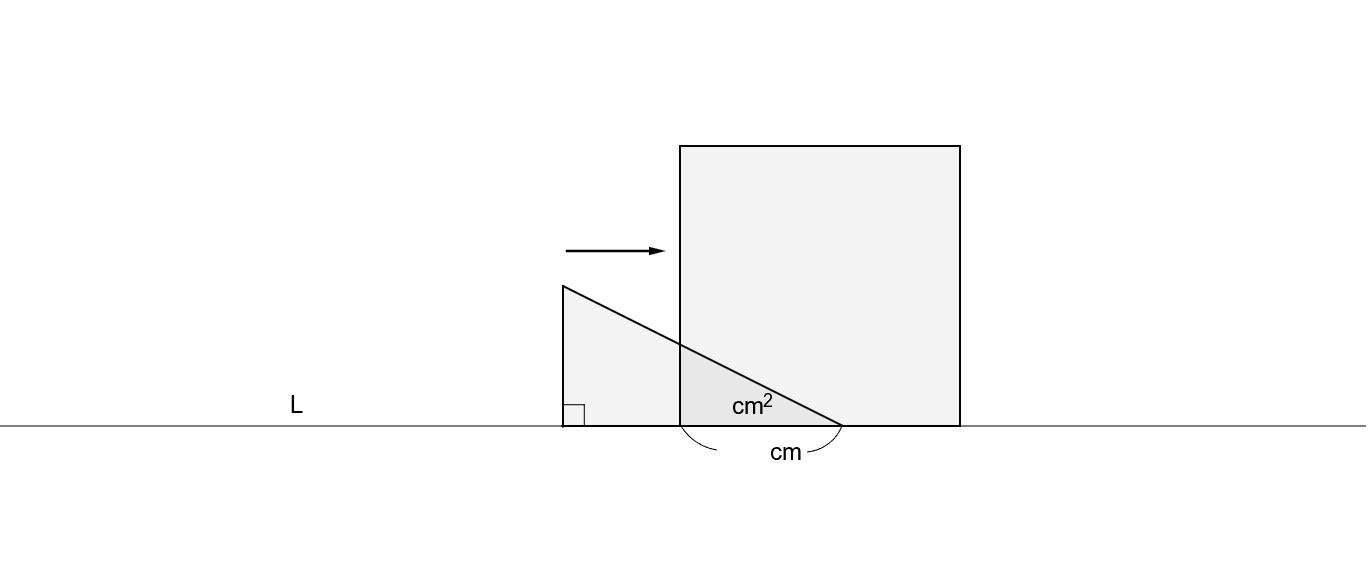
数学3 図形の中に現れる関数と相似な図形 Geogebra

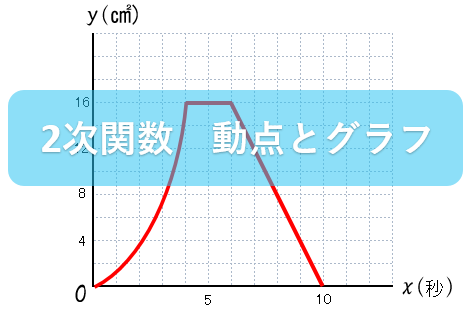
中3数学 2次関数指導案 動点とグラフの問題について丁寧な解説がたくさんある授業

数学 中3 41 二次関数の利用 一次関数とのコラボ編 Youtube

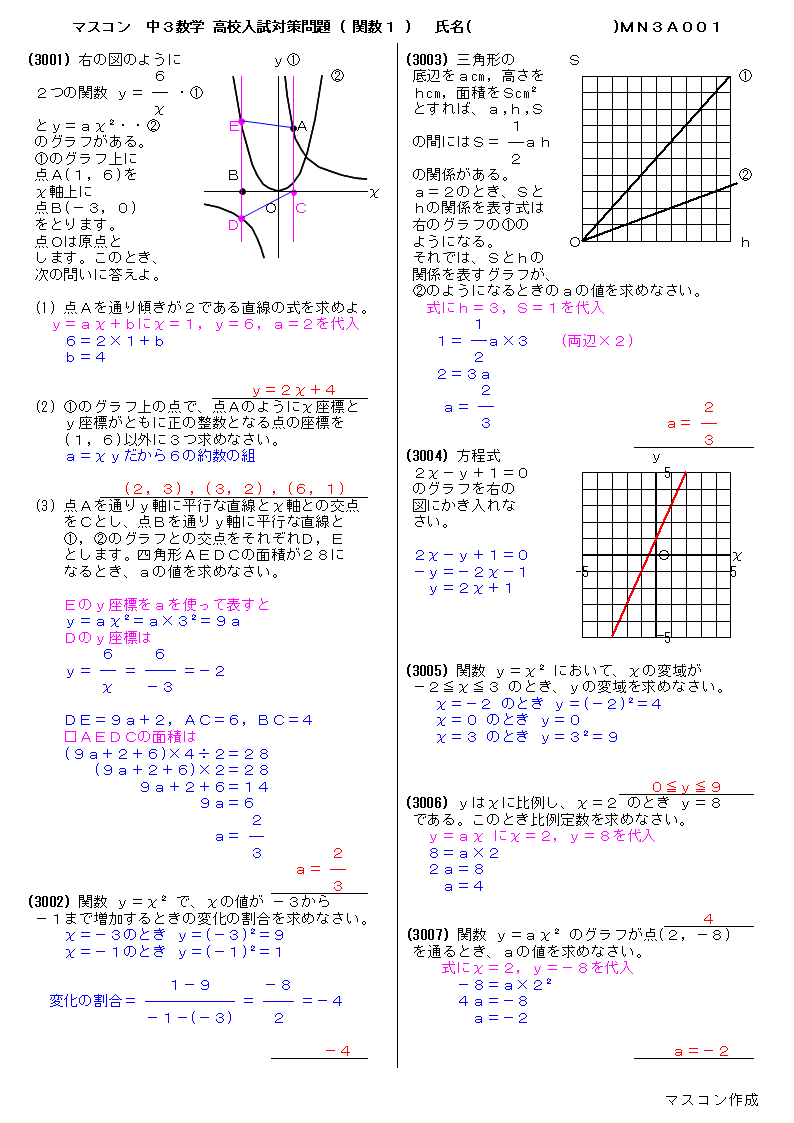
無料 中３数学 高校入試対策問題 解答プリント 312 関数

中学数学 関数とは何ものなのか Youtube

3

中学数学 関数とは何ものなのか 意味と定義を5分でふりかえる Qikeru 学びを楽しくわかりやすく

中学3年の数学 動画 二次関数の利用 一次関数とのコラボ編の問題 19ch

中学数学 二次方程式の応用問題 市川高校 一次関数 数樂管理人のブログ

中3数学 二次関数15 関数y Ax 2の利用 図形の移動 すべて無料 星組の中学数学講座

中３ 数学 関数y Ax 2 2次関数 ９分 Youtube

二次関数とグラフ 中３数学 高校数学 Irohabook

Download 中学校2年生数学 一次関数 Images For Free

中３ 関数の応用問題 数学のトリセツ ４章 が終わった人へ Youtube

ヨドバシ Com できた 中３数学 計算 関数 中学基礎がため１００ 全集叢書 通販 全品無料配達

中3数学 2次関数の利用 相似な図形の利用 相似比 3学期期始めテスト 期末テスト用 赤城 ᐡᐤᐡ

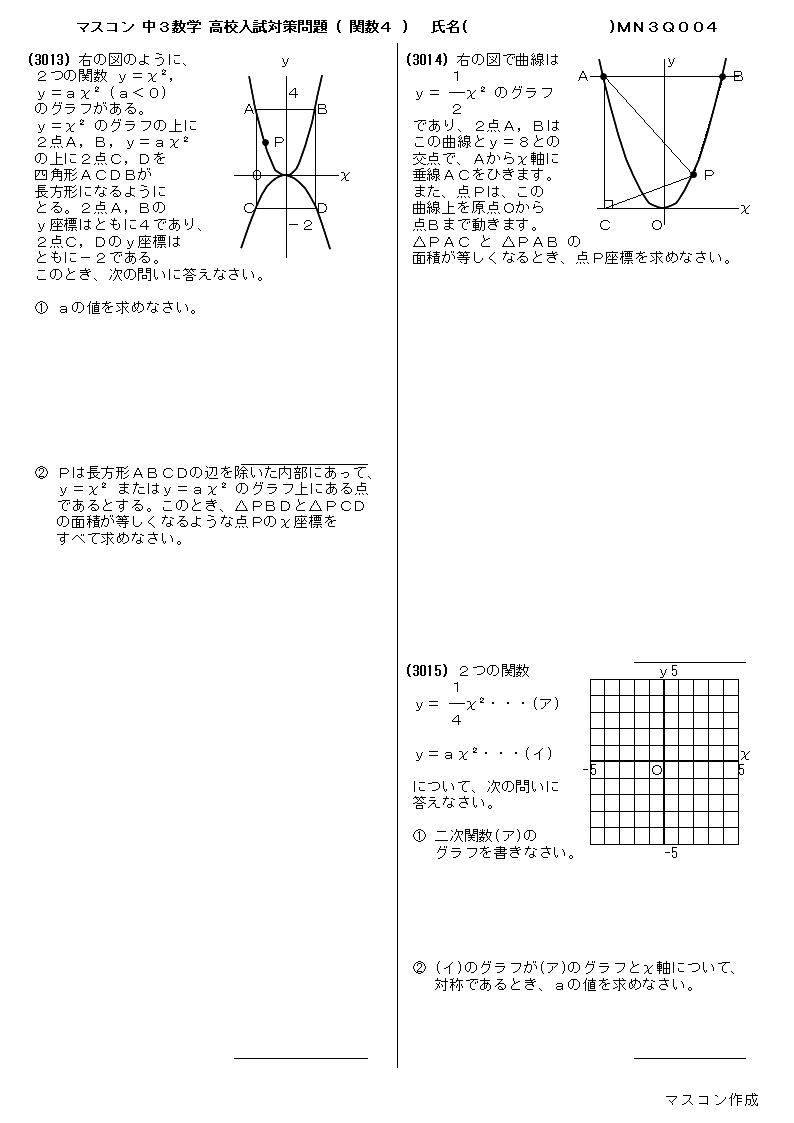
無料 中３数学 高校入試対策問題 問題プリント 315 関数４

数学 中3 39 二次関数の利用 平均の速さ編 Youtube

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

中学3年の数学 動画 二次関数の式をもとめるの問題 Y Ax Sup 2 Sup 19ch

中１ 数学 中１ ４０ 関数って Youtube

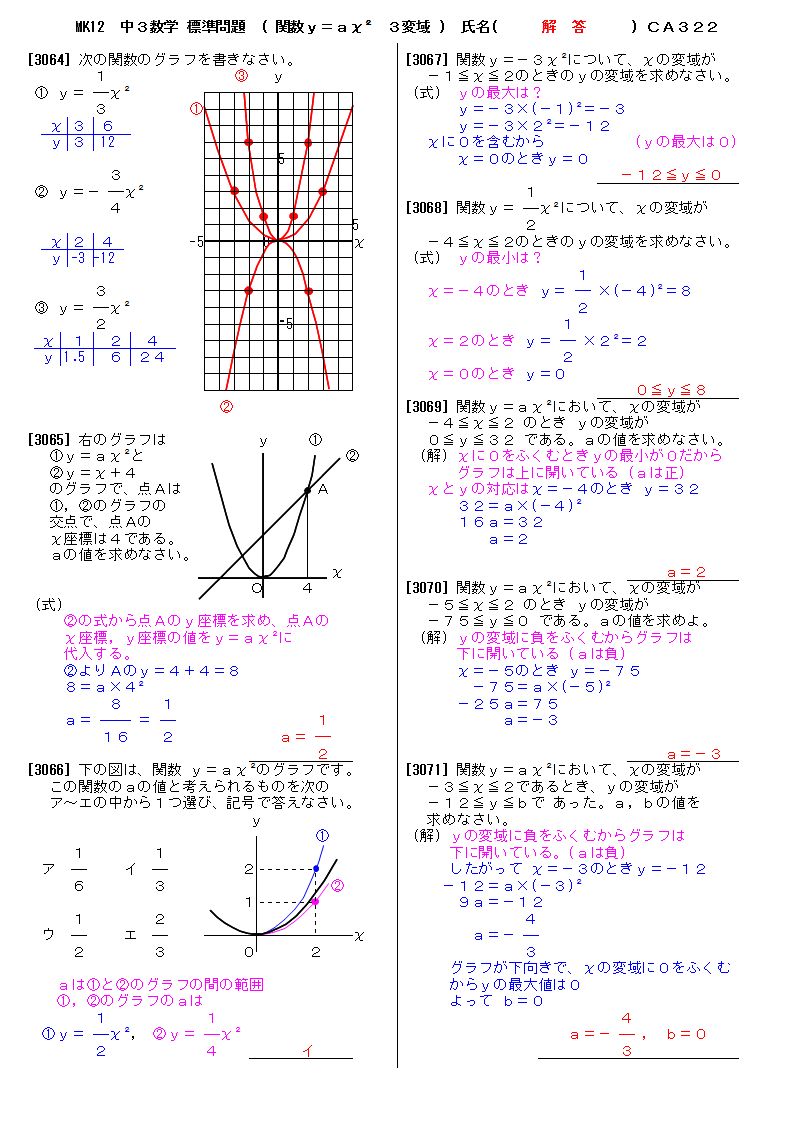
無料 中３数学 標準問題 解答プリント 関数ｙ ａx２乗 ３変域

中学3年の数学 動画 二次関数の利用 一次関数との交点編の問題 19ch

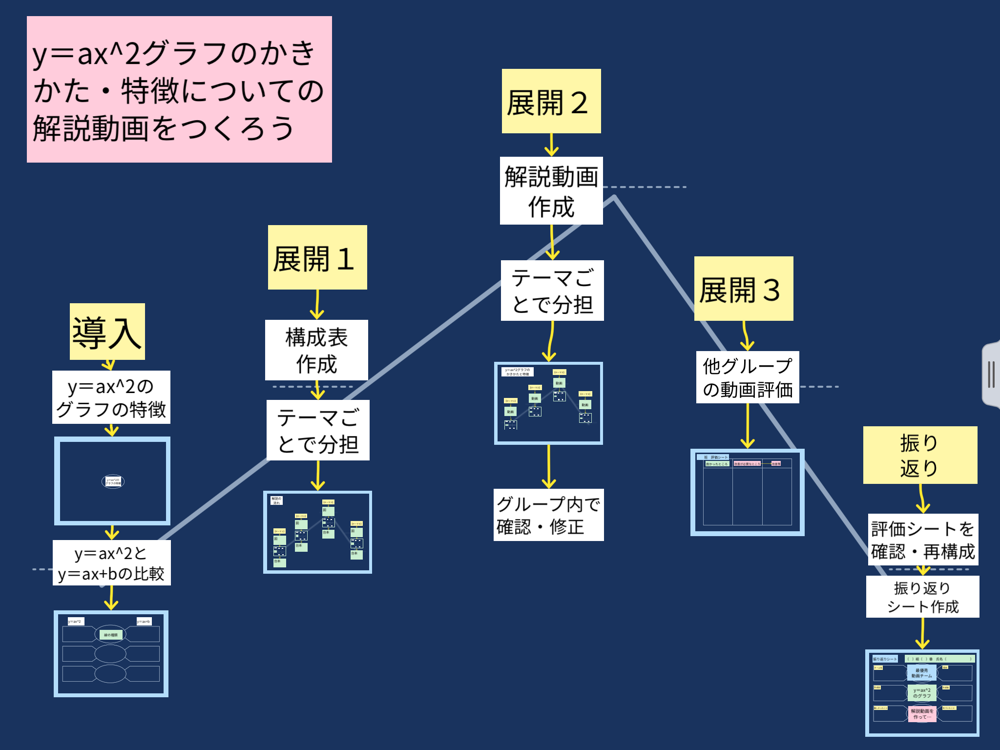
ロイロノート スクール サポートページ 中３ 算数 数学 関数 Y Ax 2グラフのかきかた 特徴について解説動画をつくろう 授業案 墨田区立桜堤中学校 岩井 洋平

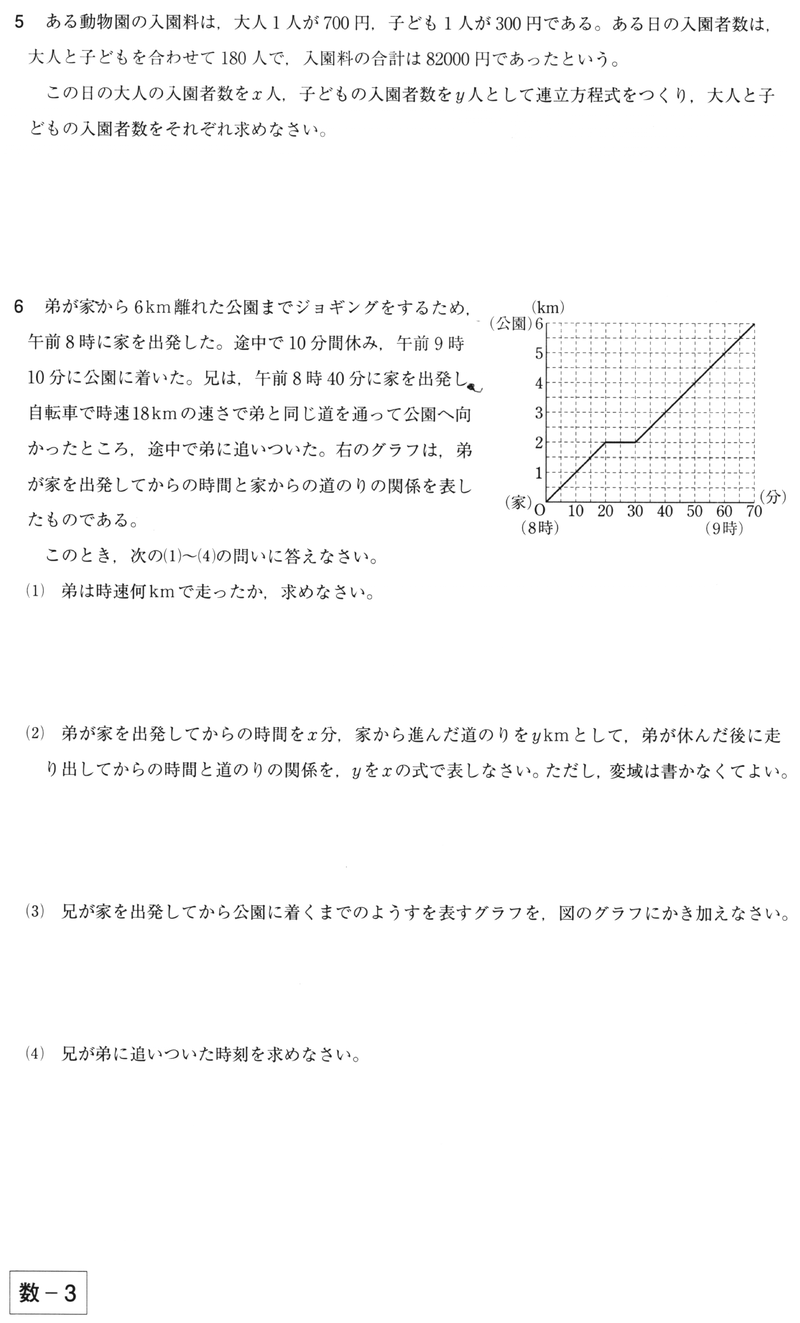
中学 数学 実力テスト 過去問 連立方程式 1次関数の利用 問題と解答 赤城 ᐡᐤᐡ

中3数学 二次関数14 関数y Ax 2の利用 動点 すべて無料 星組の中学数学講座

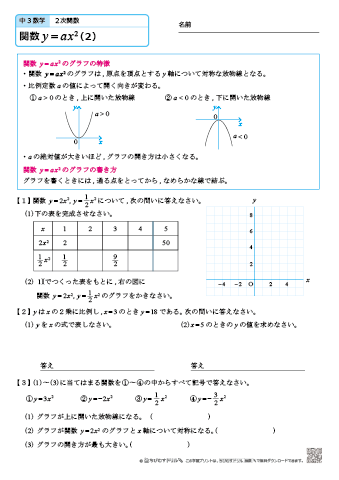
中学３年生 数学 ２次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su

中学数学発展篇方程式と関数 中1 中3 未来を切り開く学力シリーズ 改訂新版 橋野篤 Hmv Books Online

中学数学問題集 中３ ２次関数 １８ 5 中学数学高校数学個別指導in山形市 数専ゼミ

中3数学 二次関数23 関数y Ax 2の利用 いろいろな関数 すべて無料 星組の中学数学講座

無料 中３数学 発展 応用問題 解答プリント 325 関数ｙ ａx２乗 ６放物線と直線２

くもんの中学基礎がため100 中3数学 計算 関数編 平成21 23年度用 Amazon Com Books

中3数学 放物線と直線の交点 練習編 映像授業のtry It トライイット

中3数学 2次関数の変化の割合 赤城 ᐡᐤᐡ

世界一わかりやすい数学問題集中２ ３章 一次関数

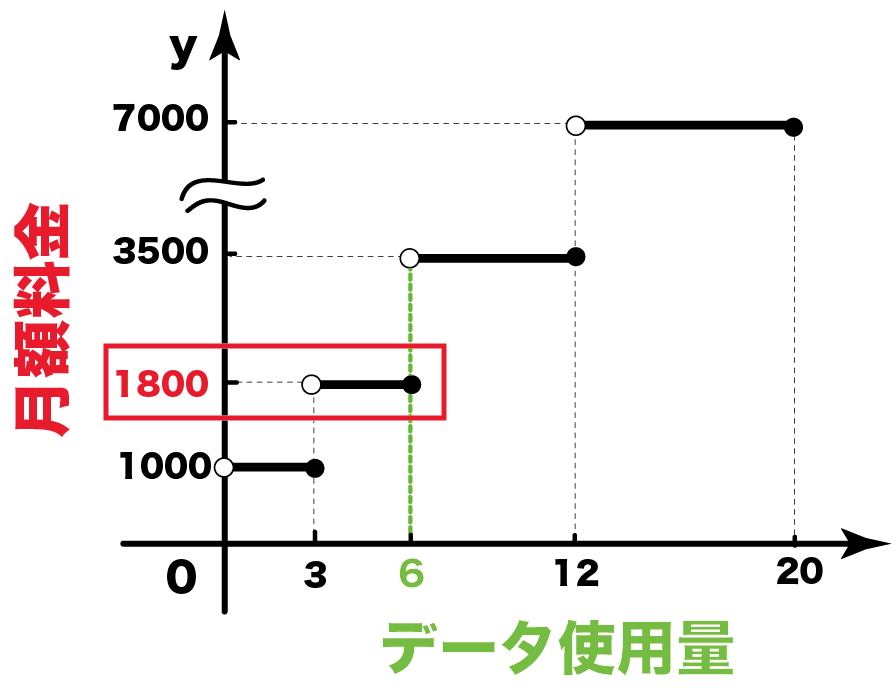
中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

中3数学 2乗に比例する関数の利用 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ

Books Kinokuniya くもんの中学基礎がため１００ 中３数学 計算 関数編 改訂新版 学習指導要領対応

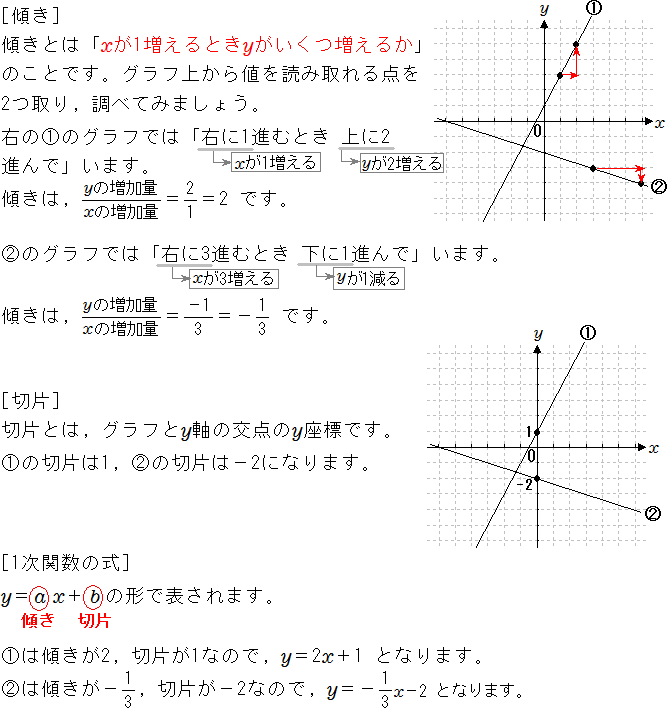
１次関数 1次関数のグラフの読み取りの基礎 中学数学 定期テスト対策サイト

かずお式中学数学ノート12 中3二次方程式 二次関数 かずお式中学数学ノートシリーズ 高橋一雄 當間光沙 本 通販 Amazon

1

中学3年の数学 動画 二次関数って の問題 比例定数 19ch

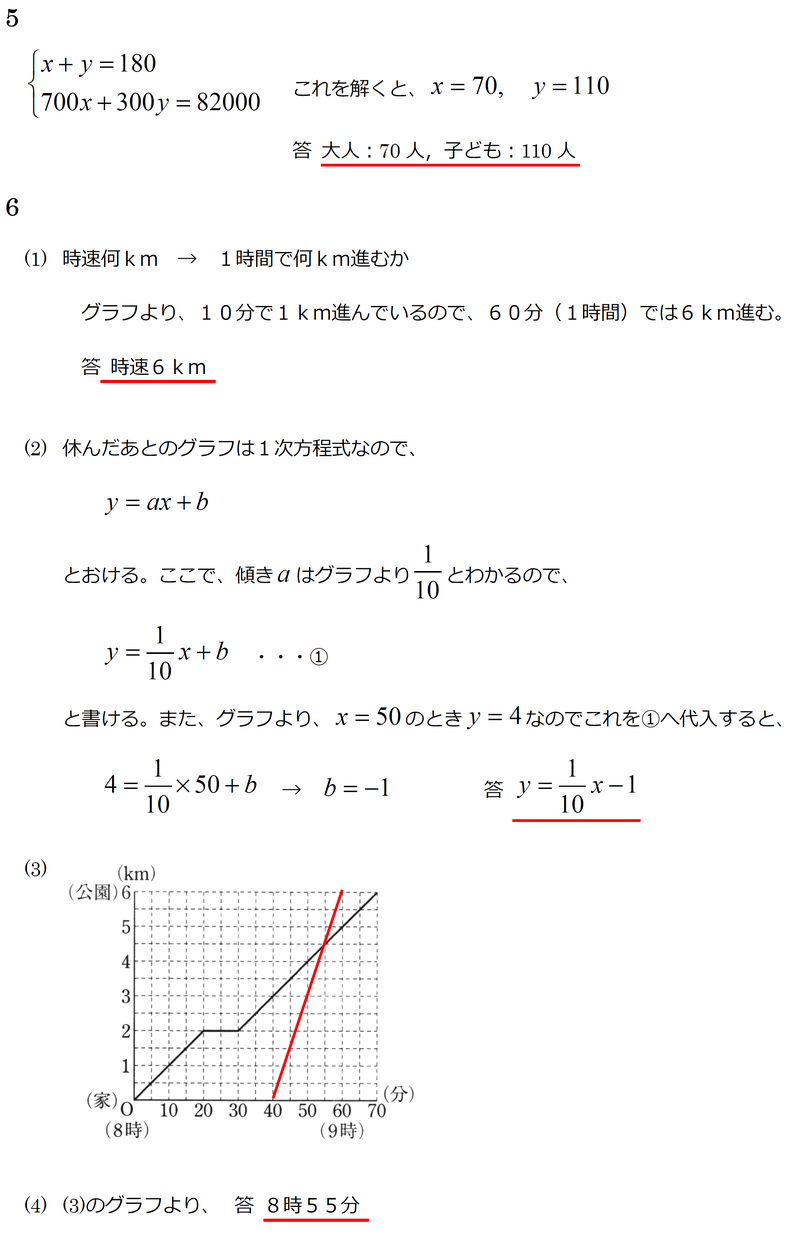
中学 数学 実力テスト 過去問 連立方程式 1次関数の利用 問題と解答 赤城 ᐡᐤᐡ

楽天市場 くもん出版 できた 中３数学 計算 関数 くもん出版 価格比較 商品価格ナビ

世界一わかりやすい数学問題集中３ ４章 二次関数

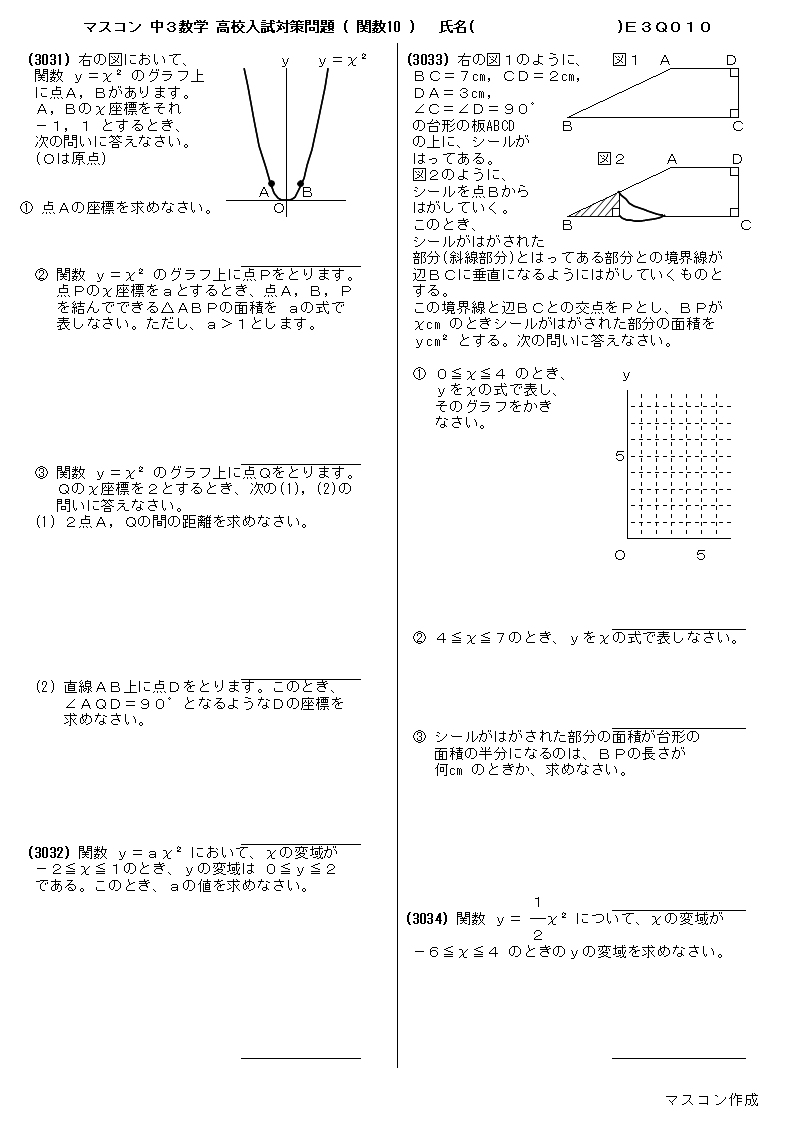
無料 中３数学 高校入試対策問題 問題プリント 321 関数10

中3数学 2乗に比例する関数 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ

無料 中３数学 高校入試対策問題 解答プリント 316 関数５

中3数学 二次関数の定期テスト対策予想問題

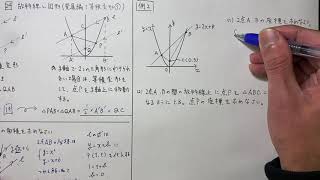
中3数学 二次関数24 三角形の面積 発展編 等積変形 すべて無料 星組の中学数学講座

中学数学問題集 中３ ２次関数 １９ 5 中学数学高校数学個別指導in山形市 数専ゼミ

楽天ブックス できた 中3数学 計算 関数 本

中学３年生 数学 ２次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中3数学 Y Ax2乗の変域の求め方を解説 数スタ

中３ 数学 関数y Ax 2 文章題１ １１分 Youtube

中学3年数学 二次関数 二次関数では必須の平方完成 やり方と成り立ちをわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト

中学3年数学 二次関数 平方完成を使って二次方程式を解く 数学の面白いこと 役に立つことをまとめたサイト

3

中学数学 関数とは何ものなのか 意味と定義を5分でふりかえる Qikeru 学びを楽しくわかりやすく

中3数学 ２次関数と等積変形の利用のポイント

数学 中2 32 一次関数の式をもとめる 基本編 Youtube

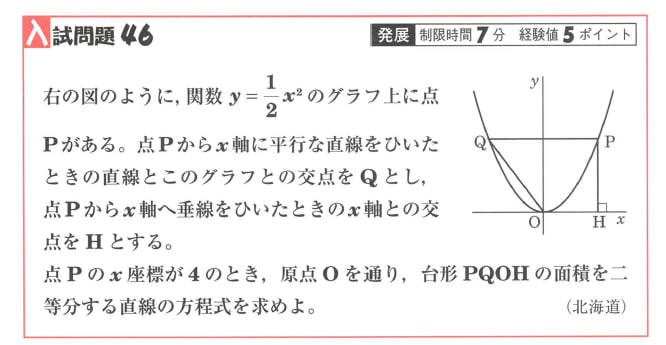
中学数学 １次関数 ２次関数 46 北海道 宮城県 高校入試問題 英語 数学 さくら教育研究所 中学 高校受験 Skredu

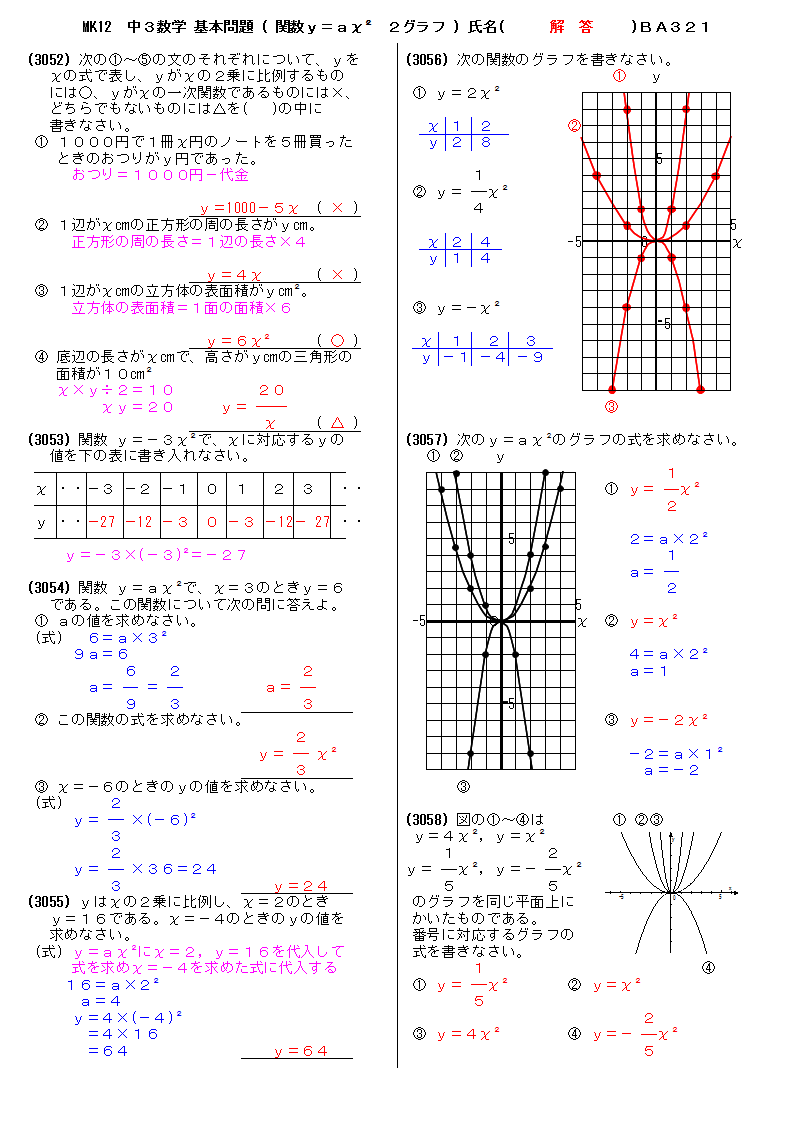
無料 中３数学 基本問題 解答プリント 321 関数ｙ ａx２ ２グラフ

数学 中2 30 一次関数のグラフを書く Youtube

Kelas 9 Catatan Tentang 数学 中３ 二次関数まとめ Clearnote

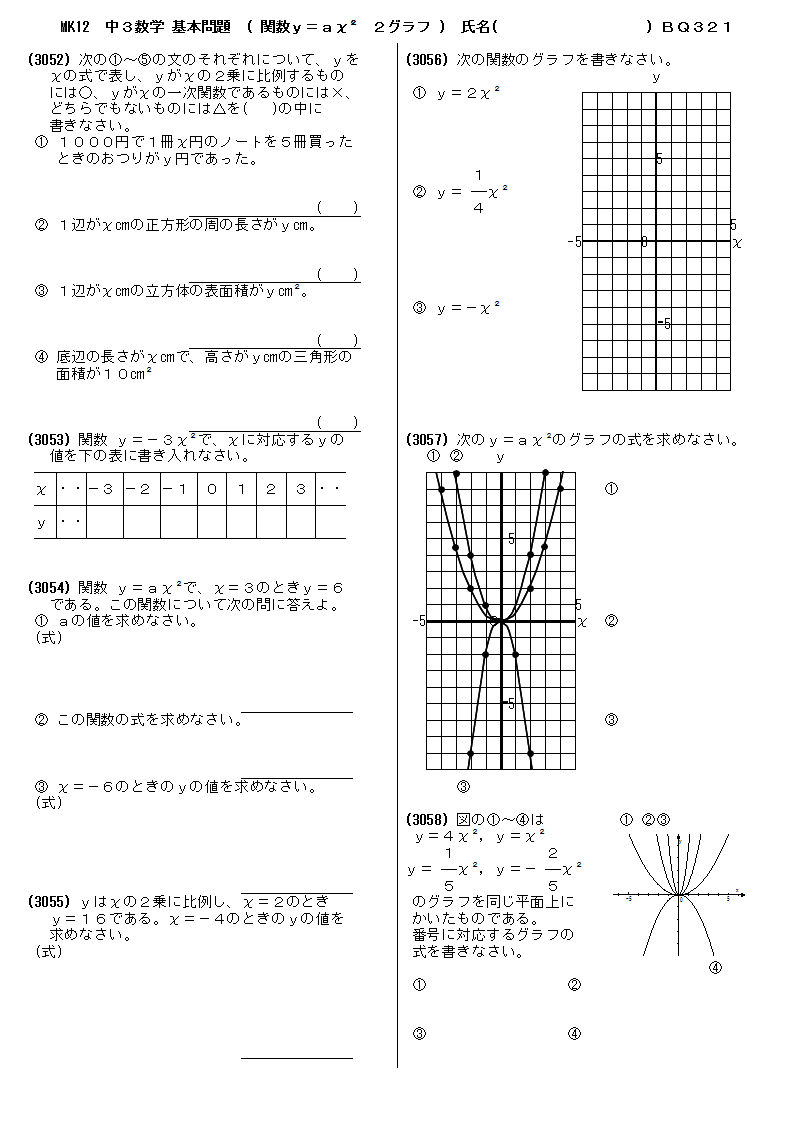
無料 中３数学 基本問題 問題プリント 321 関数ｙ ａx２ ２グラフ

中学２年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

二次方程式

スーパーステップ 中学数学 関数 資料の活用 くもん出版

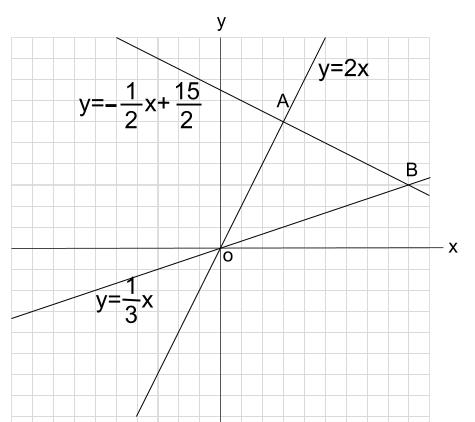
中学数学 １次関数と三角形の面積 その２ 中学数学の無料オンライン学習サイトchu Su

これで点が取れる 単元末テスト 中３数学 ４章 二次関数

中学３年生 数学 ２次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中3数学 二次関数クルクル回る問題 ブログ アビット

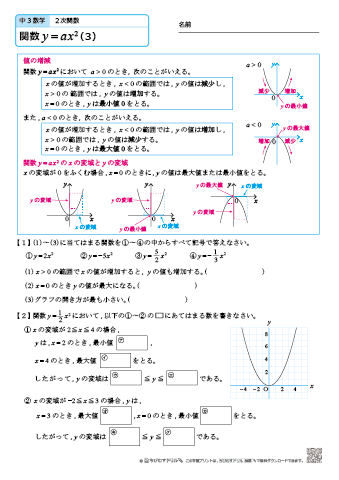
中学３年生 数学 ２次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中3数学 二次関数のグラフの特徴の定期テスト過去問分析問題 ダイスト

中3数学 2次関数の変域の求め方 赤城 ᐡᐤᐡ

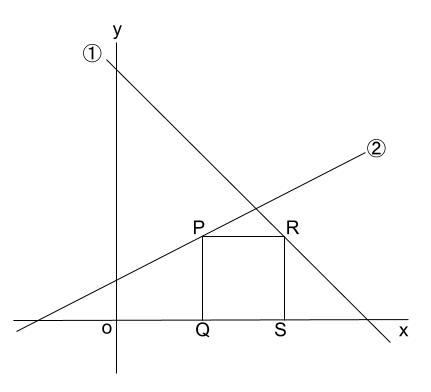
1次関数と正方形 中学数学の無料オンライン学習サイトchu Su

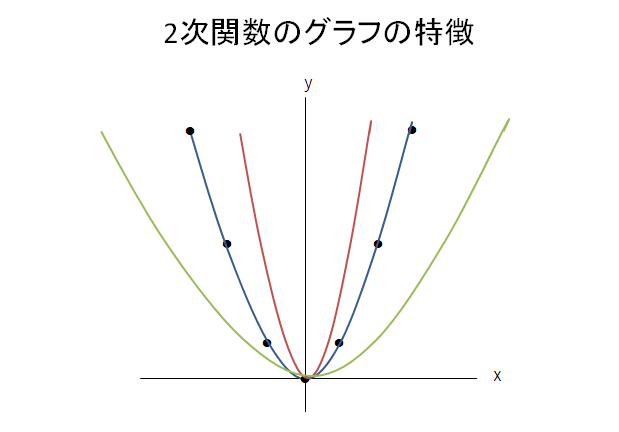
中3数学 二次関数のグラフの要点まとめノート デルココ

中３数学 ２次関数 いろいろな変域の問題 Youtube

中3数学 ２次関数のグラフの特徴と練習問題 トルテン

数学 中2 27 一次関数って Youtube

Incoming Term: 数学 中 3 関数 問題,